Variance Calculation: A Simple Guide to Measuring Consistency Without Complex Math

Ever wondered how businesses assess performance stability, track financial trends, or measure consistency in customer satisfaction? The answer lies in variance calculation—a crucial metric that helps identify how much data points deviate from the average.

Whether it’s stock prices, customer ratings, or monthly sales performance, variance provides valuable insights into predictability and risk assessment. While it may sound technical, understanding variance doesn’t require advanced math skills. In this guide, we’ll break it down in the simplest way possible—no formulas, just practical insights!

Key Takeaways

• Variance helps determine how much individual data points deviate from the mean in a dataset.
• It is calculated by averaging the squared differences between each value and the mean.
• Population variance considers all data points, while sample variance is used when analyzing a subset.
• A larger variance means greater dispersion in data, while a lower variance suggests values are closely clustered.
• Variance analysis is essential for risk assessment, performance evaluation, and decision-making across industries.

What is Variance?

Variance is a key statistical concept that measures how spread out a set of numbers is from the average (mean). It helps determine whether data points are consistent and predictable or fluctuating and uncertain.

In simple terms, variance tells us how much numbers deviate from the expected value. A low variance means that most data points are close to the average, indicating stability. A high variance suggests that values are scattered widely, making outcomes unpredictable.

Let’s break it down with a real-life example:

Imagine you’re tracking your daily coffee spending for a week:

• Monday: $5
• Tuesday: $5
• Wednesday: $4.50
• Thursday: $5
• Friday: $5.50

Here, your spending is pretty consistent—no major jumps—so the variance is low.

Now, let’s say another week looks like this:

• Monday: $3
• Tuesday: $8
• Wednesday: $2
• Thursday: $10
• Friday: $6

This time, your spending is all over the place—some days you spend barely anything, while on others, you splurge. This means the variance is high.

Why Does Variance Matter?

Variance is used in business, finance, and everyday decisions to measure stability vs. fluctuation.

Category	Impact of Low Variance	Impact of High Variance
Business	Predictable revenue, easier financial planning.	Unstable revenue, difficult to plan ahead.
Finance	Steady stock performance, lower investment risk.	Stock price fluctuations, higher investment risk.
Everyday Life	Consistent electricity bills, controlled expenses.	Unpredictable vacation spending, budgeting challenges.

1. In Business

• If a company’s monthly revenue is steady, it has low variance, making it easier to predict future profits.
• If sales swing up and down, the business has high variance, making planning harder.

2. In Finance

• Investors use variance to assess risk.
• A stock with low variance (steady growth) is less risky.
• A stock with high variance (big price swings) is unpredictable.

3. In Everyday Life

• Your monthly electricity bill likely has low variance—it stays around the same amount.
• Your vacation spending might have high variance—some trips are budget-friendly, while others break the bank!

Variance Shows Stability or Instability

• Low variance = Predictable, steady, reliable
• High variance = Unpredictable, inconsistent, risky

Even without math, variance helps you understand patterns in everything from personal finances to business trends.

Why Variance Calculation Matters?

Variance isn’t just a math concept—it’s a powerful tool that helps businesses, investors, and even everyday people make better decisions. It reveals whether things are stable and predictable or all over the place and uncertain.

Here’s why variance calculation is a big deal:

Performance Tracking: Is Your Business on the Right Track?

Every business wants consistent growth, but how do you measure it? Variance helps track performance trends in key areas like:

• Sales: If revenue jumps one month and drops the next, variance shows how stable (or unstable) your income is.
• Marketing Campaigns: If one ad gets 100 leads and another only gets 10, variance highlights inconsistency in performance.
• Employee Productivity: If one salesperson closes 20 deals a month while another closes only 5, variance reveals the gap in performance.

Why it matters?

A business with low variance in sales and marketing results can plan ahead with confidence. High variance means unpredictability, making it harder to forecast revenue or measure progress.

Risk Assessment: Is an Investment Safe or Risky?

Investors use variance to understand risk before putting money into stocks, real estate, or other assets.

• A stock that steadily increases in value has low variance, meaning it’s a safer bet.
• A stock that soars 20% one week and crashes 15% the next has high variance, meaning it’s more volatile and risky.

Why it matters?

If you’re investing for long-term growth, you might prefer assets with low variance (more stability). If you’re looking for high returns quickly, you might be okay with high variance (more risk).

Quality Control: Are Products or Services Consistently Good?

No customer wants a product that works perfectly one time and fails the next. Companies use variance to:

• Analyze product defects—are certain batches worse than others?
• Measure customer satisfaction—are reviews consistently high, or do they fluctuate?
• Improve manufacturing processes—is production quality steady, or are there frequent issues?

Why it matters?

A low variance in product quality means fewer complaints, more happy customers, and stronger brand loyalty. High variance suggests inconsistencies that might hurt reputation and sales.

Variance is everywhere—in business performance, investments, and product quality.

• Low variance = Stability & predictability
• High variance = Uncertainty & risk

Whether you’re a business owner, investor, or consumer, understanding variance helps you make smarter decisions.

The No Math Approach to Understanding Variance Calculation

You don’t need to be a math genius to understand variance calculation. Instead of crunching numbers, you can look at patterns and trends. Here’s a quick and easy way to analyze variance calculation without using a calculator.

Step 1: Identify Your Data

The first step is to decide what you’re measuring. Variance applies to almost anything that involves numbers, such as:

• Monthly revenue – Are sales numbers steady or unpredictable?
• App downloads – Do user downloads remain consistent or fluctuate wildly?
• Employee productivity – Are work output levels stable, or do they vary significantly?

The key is to choose a dataset that matters to your business, finances, or daily life.

Step 2: Estimate the Average

Instead of calculating an exact average (mean), just ask “What’s the usual trend?”

For example:

• If most of your customer reviews are around 4 stars, that’s your average rating.
• If your monthly revenue typically stays near $10,000, that’s your expected income level.

No need for formulas—just a simple observation of where most numbers fall.

Step 3: Look at the Spread

Now, check how much your data fluctuates:

• If the numbers are close to the average, you have low variance (predictable and stable).
• If the numbers are all over the place, you have high variance (unpredictable and inconsistent).

Low Variance: If your revenue is usually between $9,800 and $10,200, it’s stable (low variance).
High Variance: If you make $5,000 one month, $15,000 the next month, and then $7,000, it’s all over the place (high variance).

Step 4: Make Better Decisions

Once you understand whether your variance is high or low, you can make informed choices.

• Low Variance = Stability & Predictability
  • Great for businesses that need consistent revenue.
  • Reliable investment choices.
  • Steady product quality and customer experience.
• High Variance = Risk & Inconsistency
  • It can be risky for businesses (it is hard to forecast profits).
  • Might indicate unpredictable investments.
  • Suggests quality issues in product manufacturing or customer service.

Variance isn’t just a math term—it’s a tool that helps you understand patterns and make smarter decisions.

Real-Life Examples of Variance Calculations (No Math Required)

Variance is everywhere in the real world, influencing decisions in business, marketing, investing, and customer satisfaction. Understanding variance calculation helps businesses and individuals assess stability, track patterns, and predict future trends.

Below are practical examples of how variance plays a role in everyday scenarios.

1. E-Commerce: Spotting Product Quality Issues

In online retail, product return rates provide valuable insights into customer satisfaction and quality control. Suppose an e-commerce company tracks return rates for a best-selling product over six months:

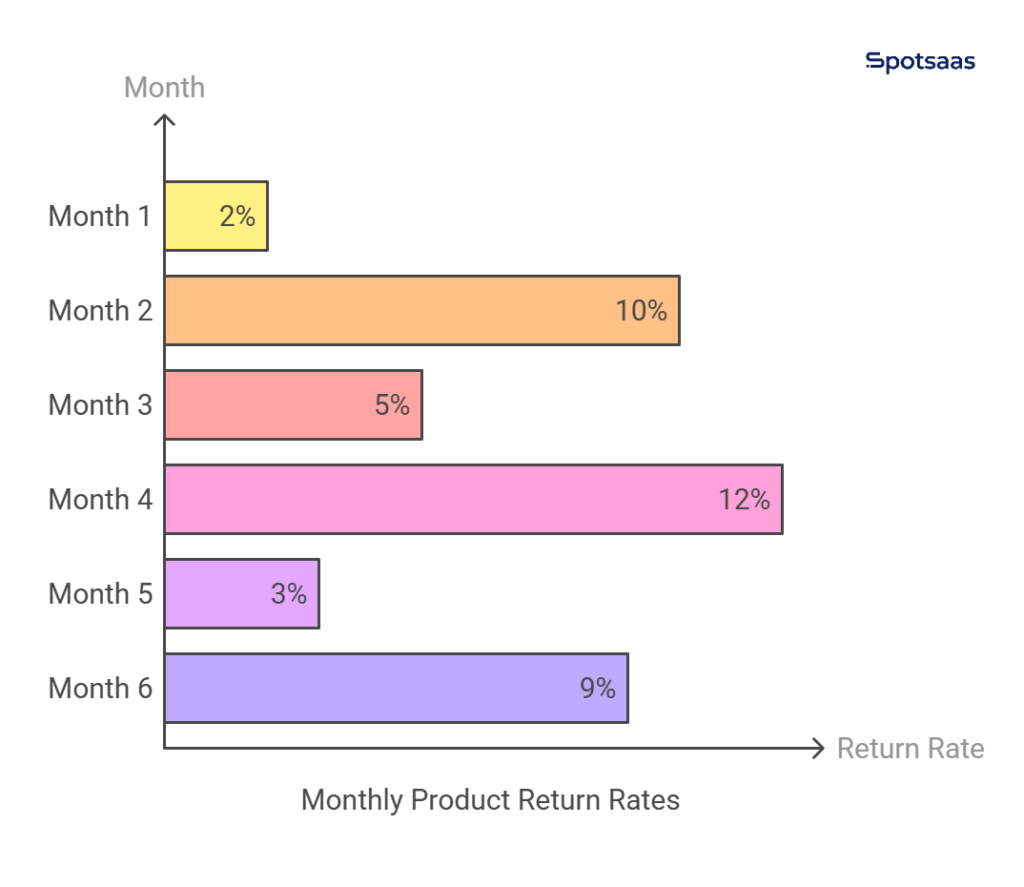
• Month 1: 2% returns
• Month 2: 10% returns
• Month 3: 5% returns
• Month 4: 12% returns
• Month 5: 3% returns
• Month 6: 9% returns

This inconsistency indicates high variance, meaning the product is experiencing quality fluctuations or issues in different batches. Some customers may receive well-made products, while others get defective ones, leading to unpredictable return rates.

If the return rate consistently stays between 2% and 4%, the variance is low, suggesting a stable product quality with fewer unexpected issues. This data helps businesses identify manufacturing problems, improve product consistency, and enhance customer satisfaction.

2. Marketing Campaigns: Measuring Campaign Consistency

Marketing teams use variance to evaluate the effectiveness of their strategies. Consider an email marketing campaign where open rates fluctuate over multiple weeks:

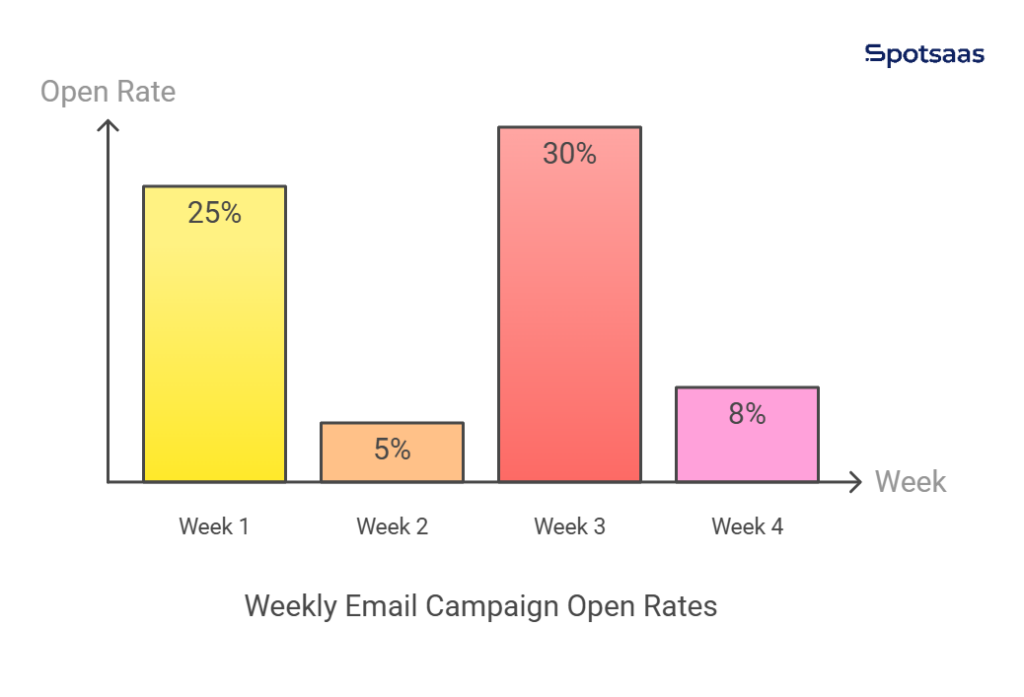
• Week 1: 25% open rate
• Week 2: 5% open rate
• Week 3: 30% open rate
• Week 4: 8% open rate

A high variance in open rates suggests that the campaign’s effectiveness is inconsistent. Some emails resonate with the audience, while others fail to attract engagement. This could be due to variations in subject lines, audience targeting, or content relevance.

If open rates remain steady between 20% and 25%, it means the variance is low, and the campaign is consistently performing well. Marketers use this data to optimize content, test subject lines, and refine targeting for better engagement.

3. Stock Market: Understanding Risk in Investments

Investors use variance to assess risk and volatility in stock prices. Suppose an investor is analyzing two stocks:

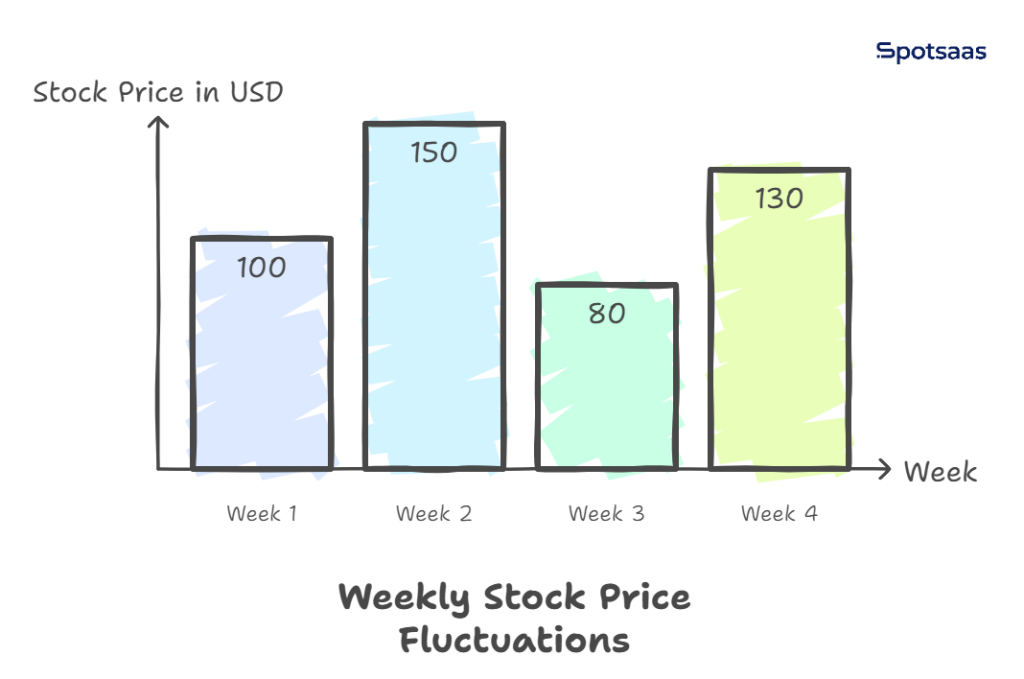
Stock A – High Variance

• Week 1: $100
• Week 2: $150
• Week 3: $80
• Week 4: $130

This stock experiences wild price fluctuations, making it unpredictable and riskier. High variance stocks can lead to large gains but also pose significant risks.

Stock B – Low Variance

• Week 1: $100
• Week 2: $105
• Week 3: $102
• Week 4: $107

This stock grows at a steady, predictable pace with low variance, making it a safer choice for long-term investors. Companies with low variance stock performance are generally stable and considered lower-risk investments.

Investors use variance analysis to decide whether they want to invest in high-risk, high-reward stocks or prefer steady, lower-risk investments.

Why Variance Matters in Real Life

Variance is not just a statistical measure—it plays a crucial role in business decision-making, marketing effectiveness, financial risk assessment, and product quality control. Understanding variance helps businesses and individuals:

• Identify inconsistencies in sales, returns, and customer behavior.
• Improve marketing strategies by measuring fluctuations in engagement and conversions.
• Evaluate financial risks before making investments.
• Ensure product quality remains stable and meets customer expectations.

By recognizing whether variance is high or low in any dataset, businesses and individuals can make more informed decisions without complex calculations.

How to Estimate Variance Calculation Without a Calculator

Understanding variance calculation doesn’t require complex math formulas or number crunching. You can estimate variance quickly by looking at patterns and comparing data sets. Here are three simple ways to assess variance without using a calculator.

Method	Description	Example
Rule of Thumb	Check if data feels stable or fluctuates.	Bill: $90-$110 (low) vs. $50, $200, $120 (high).
Sorting Data	Arrange numbers; close values mean low variance.	Traffic: 95, 100, 105 (low) vs. 50, 200, 75 (high).
Comparison Trick	Compare datasets; smaller changes mean lower variance.	Stable revenue: $9,800-$10,050 vs. $5,000-$15,000.

Rule of Thumb: Identify Stability vs Unpredictability

The easiest way to estimate variance is by asking:
“Does my data feel stable, or does it swing drastically?”

• If values stay relatively close to each other, variance is low.
• If numbers fluctuate wildly, variance is high.

Example:

Imagine tracking your monthly electricity bill:

• If your bill is between $90 and $110 every month, it’s predictable—low variance.
• If your bill is $50 one month, $200 the next, then $120, it’s unpredictable—high variance.

This simple observation helps you spot patterns without needing calculations.

Visual Check: Sorting Your Data

Sometimes, simply organizing your numbers in order makes variance easy to spot.

How to do it:

1. List the data points in ascending order.
2. Check how closely the values are grouped together.
   • If numbers are tightly packed, variance is low.
   • If numbers jump unpredictably, variance is high.

Example:

A retail store tracks daily foot traffic over a week:

Low Variance (Predictable Days)

• 95, 100, 105, 102, 98, 101, 99

All numbers are close to each other, meaning foot traffic is steady.

High Variance (Unpredictable Days)

• 50, 200, 75, 300, 90, 180, 120

Here, the customer count varies significantly, making it hard to predict trends.

Sorting data this way visually highlights variance and helps businesses spot inconsistencies.

The Comparison Trick: Spot the Differences

Another way to estimate variance is by comparing two data sets. The question to ask is:
“Which set feels more stable?”

Example: Business Revenue Analysis

Two businesses track their monthly revenue for six months.

Company A (Low Variance – Stable Revenue):

• $9,800, $9,750, $9,900, $10,050, $9,950, $9,870

Company B (High Variance – Unpredictable Revenue):

• $5,000, $12,500, $7,800, $15,000, $6,200, $10,900

Which one feels more stable?

• Company A has a consistent revenue stream, meaning its variance is low.
• Company B has unpredictable revenue swings, meaning it has high variance.

This method works in various situations:

• Comparing marketing campaign engagement rates
• Analyzing customer return rates for different products
• Evaluating performance scores of employees

Final Thoughts

Estimating variance doesn’t require calculations—just an observant eye and a structured approach.

• Look at patterns—is the data stable or unpredictable?
• Sort numbers—if they are clustered, variance is low.
• Compare datasets—which one looks more consistent?

By following these simple methods, you can understand variance instantly and use it for better decision-making in business, finance, and daily life.

Conclusion

Variance is not just a mathematical concept—it’s a powerful tool for decision-making in business, finance, marketing, and everyday life. It helps identify patterns, measure consistency, and evaluate risks without requiring complex math formulas.

On the other hand, high variance signals fluctuate and are uncertain. A company experiencing inconsistent sales, an ad campaign with unpredictable results, or a stock with extreme price swings may require closer monitoring and adjustments.

By estimating variance without a calculator, businesses and individuals can spot trends, identify risks, and optimize strategies effectively. Simply observing patterns, sorting data, and making comparisons can reveal valuable insights.

Who benefits from understanding variance calculation?

• Business owners looking to track performance and revenue trends.
• Investors assessing the risk of volatile assets.
• Marketers optimizing campaigns based on engagement consistency.
• Manufacturers maintaining product quality control.

Instead of focusing on formulas, the key is to ask:
“Is this data stable and predictable, or does it fluctuate too much?”

Mastering variance empowers better decision-making, helping individuals and businesses reduce uncertainty, improve forecasting, and create more reliable strategies—all without needing advanced math skills.

Frequently Asked Questions